排列组合复习回顾
1.(排列问题)有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.
(1)选其中5人排成一排;[来源:学科网]
(2)排成前后两排,前排3人,后排4人;
(3)全体排成一排,甲不站排头也 不站排尾;
不站排尾;
(4)全体排成一排,女生必须站在一起;
(5)全体排成一排,男生互不相邻;
(6)全体排成一排,甲、乙两人中间恰好有3人;
(7)全体排成一排,甲必须排在乙前面;
(8)全部排成一排,甲不排在左端,乙不排在右端.
是排列.有A75=7×6×5×4×3=2 520(种).
(2)分两步完成,先选3人排在前排,有A73种方法,余下4人排在后排,有A44种方法,故共有A73·A44=5 040(种).事实上,本小题即为7人排成一排的全排列,无任何限制条件.
(3)(优先法)
方法一:甲为特殊元素.先排甲,有5种方法;其余6人有A66种方法,故共有5×A66=3 600种.
方法二:排头与排尾为特殊位置.排头与排尾从非甲的6个人中选2个排列,有A62种方法,中间5个位置由余下4人和甲进行全排列,有A55种方法,共有A62×A55=3 600种.
(4)(捆绑法)将女生看成一个整体,与3名男生在一起进行全排列,有A44种方法, 再将4名女生进行全排列,也有A44种方法,故共有A44×A44=576种.
再将4名女生进行全排列,也有A44种方法,故共有A44×A44=576种.
(5)(插空法)男生不相邻,而女生不作要求,所以应先排女生,有A44种方法,再在女生之间及首尾空出的5个空位中任选3个空位排男生,有A53种方法,
故共有A44×A53=1 440种.
(6)(捆绑法)把甲、乙及中间3人看作一个整体,第一步先排甲乙两人,有A22种方法;第二步从余下5人中选3人排在甲乙中间,有A53种;第三步把这个整体与余下2人进行全 排列,有A33种方法.故共有A22·A53·A33=720种.
排列,有A33种方法.故共有A22·A53·A33=720种.
(7)(消序法)=2 520.
(8)(间接法)A77-2A66+A55=3 720. 位置分析法:分甲在排尾与不在排尾两类.
2.(组合问题)7名男生5名女生中选取5人,分别求符合下列条件的选法总数有多少种?
(1)A,B必须当选;
(2)A,B必不当选;
(3)A,B不全当选;
(4)至少有2名女生当选;
(5)选取3名男生和2名女生分别担任班长、体育委员等5种不同的工作,但 体育委员必须由男生担任,班长必须由女生担任.
体育委员必须由男生担任,班长必须由女生担任.

【解题技巧】组合问题常有以下 两类题型
两类题型
(1)“含有”或“不含有”某些元素的组合题型;“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.
(2)“至少”或“最多”含有几个元素的组合题型:解这类题必须十分重视“至少”与“最多”这两个关键词的含义,谨防重复与漏解,用直接法和间接法都可以求解,通常用直接法,分类复杂时,考虑逆向思维,用间接法处理.
随堂探究
一、排列组合混合问题“先选后排”
1、从4名男生和3名女生中选3人,分别从事3项不同的工作,若这3人中只有一名女生,则选派方案有_____种。
2、有5个不同的小球,装入4个不同的盒内,每盒至少装一个球,共有_______种不同的装法。
3、一个班有6名战士,其中正副班长各1人现从中选4人完成四种不同的任务,每人完成一种任务,且正副班长有且只有1人参加,则不同的选法有________种。
二、特殊元素(或位置) “优先法”
4、用0,2,3,4,5,五个数字,组成没有重复数字的三位数,其中偶数共有________个。
5、在由数字0、1、2、3、4、5所组成的没有重复数字的四位数中,不能被5整除的数共有_______个。
6、从6名短跑运动员中选出4人参加4×100米接力赛,如果甲、乙两人都不跑第一棒,那么不同的参赛方案有( )
A.180种
B.240种
C.300种 D.360种
三、相邻问题“捆绑法”
7、6个人排成一排,甲、乙二人必须相邻的排法有______种。
8、6名同学站成一排照毕业相,要求甲不站在两侧,而且乙和丙相邻、丁和戊相邻,则不同的站法种数为( )
A.60 B.96 C.48 D.72
9、有6个座位连成一排,现有3人入座,则恰有两个空位相邻的不同坐法的种数是( )
A.36
B.48 C.72
D.120
四、不相邻问题“插空法”
10、七个人并排站成一行,如果甲乙两个必须不相邻,那么不同排法的种数是( )
A.1440
B.3600 C.4820 D.4800
11、用1,2,3,4,5,6,7,8组成没有重复数字的八位数,其中1与2相邻、3与4相邻、5与6相邻、7与8不相邻的八位数共有
个.
五、至多、至少问题“总体淘汰法”(正难则反)
12、在100件产品中有6件次品,现从中任取3件产品,至少有1件次品的不同取法的种数是( )
A.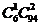 B.
B.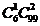 C.
C.
 D.
D.
13、从4台甲型和5台乙型电视机中任取出3台,其中至少要甲型和乙型电视机各一台,则不同取法共有( )
A.140
B.80种
C.70种
D.35种
六、分组与分配问题(均匀分组消序、先分组再分配)
14、6本不同的书,按以下要求各有多少种分法?
⑴平均分成三组;
⑵分成1本,2本、3本三组;
⑶平均分给甲、乙、丙三人;
⑷分给甲、乙、丙三人,一人拿1本,一人拿2本、一人拿3本;
⑸甲得一本,乙得二本,丙得三本.
15、某学校为了更好的培养尖子生,使其全面发展,决定由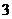 名教师对
名教师对 个尖子生进行“包教”,要求每名教师的“包教”学生不超过
个尖子生进行“包教”,要求每名教师的“包教”学生不超过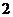 人,则不同的“包教”方案有( )
人,则不同的“包教”方案有( )
A.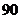 B.
B.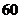 C.
C.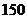 D.
D.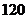
16、5本不同的书全部分给4个学生,每个学生至少一本,不同的分法种数为( )
A、480 种
B、240种
C、120种
D、96种
17、某交通岗共有3人,从周一到周日的七天中,每天安排一人值班,每人至少值2天,其不同的排法共有( )种.
A、5040 B、1260 C、210
D、630
七、定序问题“消序法”
18、3男3女排成一排,若3名男生身高不相等,则按从高到低的一种顺序站的站法有______种。
19、由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的六位数共有 个.
八、染色问题分类法

20、如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有 种.
若有5种颜色呢?
 21、如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法共有( )
21、如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法共有( )
A.288种 B.264种 C.240种
D.168种
课后作业:见校本提纲